1835: 【NOIP2020-T3】移球游戏
[Creator : ]
Submit
Description
小C正在玩一个移球游戏,他面前有n+1根柱子,柱子从1∼n+1编号,其中1号柱子、2号柱子、···、n号柱子上各有m个球,它们自底向上放置在柱子上,n+1号柱子上初始时没有球。这n×m个球共有n种颜色,每种颜色的球各m个。
初始时一根柱子上的球可能是五颜六色的,而小C的任务是将所有同种颜色的球移到同一根柱子上,这是唯一的目标,而每种颜色的球最后放置在哪根柱子则没有限制。
小C可以通过若干次操作完成这个目标,一次操作能将一个球从一根柱子移到另一根柱子上。更具体地,将x号柱子上的球移动到y号柱子上的要求为:
1.x号柱子上至少有一个球;
2.y号柱子上至多有m−1个球;
3.只能将x号柱子最上方的球移到y号柱子的最上方。
小C的目标并不难完成,因此他决定给自己加加难度:在完成目标的基础上,使用的操作次数不能超过820000。换句话说,小C需要使用至多820000次操作完成目标。
小C被难住了,但他相信难不倒你,请你给出一个操作方案完成小C的目标。合法的方案可能有多种,你只需要给出任意一种,题目保证一定存在一个合法方案。
初始时一根柱子上的球可能是五颜六色的,而小C的任务是将所有同种颜色的球移到同一根柱子上,这是唯一的目标,而每种颜色的球最后放置在哪根柱子则没有限制。
小C可以通过若干次操作完成这个目标,一次操作能将一个球从一根柱子移到另一根柱子上。更具体地,将x号柱子上的球移动到y号柱子上的要求为:
1.x号柱子上至少有一个球;
2.y号柱子上至多有m−1个球;
3.只能将x号柱子最上方的球移到y号柱子的最上方。
小C的目标并不难完成,因此他决定给自己加加难度:在完成目标的基础上,使用的操作次数不能超过820000。换句话说,小C需要使用至多820000次操作完成目标。
小C被难住了,但他相信难不倒你,请你给出一个操作方案完成小C的目标。合法的方案可能有多种,你只需要给出任意一种,题目保证一定存在一个合法方案。
Input
第一行两个用空格分隔的整数n,m。分别表示球的颜色数、每种颜色球的个数。
接下来n行每行m个用单个空格分隔的整数,第i行的整数按自底向上的顺序依次给出了i号柱子上的球的颜色。
接下来n行每行m个用单个空格分隔的整数,第i行的整数按自底向上的顺序依次给出了i号柱子上的球的颜色。
Output
本题采用自定义校验器(specialjudge)评测。
你的输出的第一行应该仅包含单个整数k,表示你的方案的操作次数。你应保证0≤k≤820000。
接下来k行每行你应输出两个用单个空格分隔的正整数x,y,表示这次操作将x号柱子最上方的球移动到y号柱子最上方。你应保证1≤x,y≤n+1且x≠y。
你的输出的第一行应该仅包含单个整数k,表示你的方案的操作次数。你应保证0≤k≤820000。
接下来k行每行你应输出两个用单个空格分隔的正整数x,y,表示这次操作将x号柱子最上方的球移动到y号柱子最上方。你应保证1≤x,y≤n+1且x≠y。
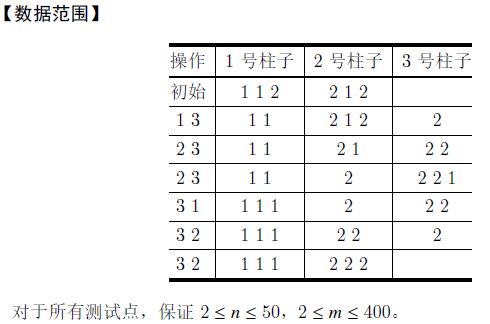
Sample Input Copy
2 3
1 1 2
2 1 2
Sample Output Copy
6
1 3
2 3
2 3
3 1
3 2
3 2
HINT